More Information
Submitted: September 23, 2024 | Approved: October 05, 2024 | Published: October 07, 2024
How to cite this article: Dong-Mei B, Zhong-Sheng G, Man-Cai G. Forecasting Soil Moisture in Caragana Shrubland Using Wavelet Analysis and NARX Neural Network. Arch Case Rep. 2024; 8(3): 087-091. Available from: https://dx.doi.org/10.29328/journal.acr.1001103
DOI: 10.29328/journal.acr.1001103
Copyright License: © Dong-Mei B, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Semi-arid loess hilly region; Caragana; Soil water; Wavelet analysis; NARX recurrent neural network; Soil moisture forecast; High-quality development
Forecasting Soil Moisture in Caragana Shrubland Using Wavelet Analysis and NARX Neural Network
Bai Dong-Mei1, Zhong-Sheng Guo1,2* and Man-Cai Guo1
1Northwest A & F University, Yangling, China 712100, China
2Institute of Soil and Water Conservation, Chinese Academy of Science and
Department of Water Resoureces, Yangling 712100, China
*Address for Correspondence: Zhong-Sheng Guo, Institute of Soil and Water Conservation, Chinese Academy of Science and Department of Water Resoureces, Yangling 712100, China, Email: [email protected]
It is important for sustainable use of soil water resource and high-quality development to forecast the soil moisture in forestland of water-limited regions. There are some soil water models. However, there is not the best model to forecast the change of soil moisture in the caragana shrubland. In this paper, the plant water relationship has been investigated at the same time for a long term in the caragana shrubland of semiarid region of the Loess Plateau of China. The data of soil moisture was divided and then NARX neural network was used to build model I and model II. For model I, low frequency component was the input variable, and for model II, low frequency component and high frequency component were predicted. The results showed the average relative error for model I is 3.5% and for model II is 0.3%. The average relative error of predicted soil moisture in 100 cm layer using model II is 0.8%, then soil water content in the 40 cm and 200 cm soil depth is selected and the forecast errors are 4.9% and 0.4%. The results showed that using model II to predict soil water is well Predicting soil water using model II will be important for sustainable use of soil water resource and high-quality development.
Soil moisture is one of the most basic elements of the soil fertility and the foundation for the crop fertility and high-quality development. The soil water resources are the soil water storage in a given soil depth, and soil water resources use limit by plant refers to the amount of water stored within the maximum infiltration depth, in which the soil moisture content in each layer is equal to the withering coefficient. When soil water resources in the maximum infiltration depth reduce to the soil water resources use limit by plant, soil drought is serious, which cause serious soil degradation, vegetation decline and crop failure because the limit of soil water carrying capacity for vegetation. At this stage of plant growth, the plant water relationship has to be regulated and to get maximum yield and service and carry out high-quality development. So, soil moisture has been highly considered. Predicting the dynamics of soil moisture is the foundation for sustainable use of soil water resources and soil water management, drought assessment and yield estimation. There are different kinds of soil moisture models such as water balance model, the SPAC water transport model, the SPAC water heat transport model, the mathematical statistics model, the random water balance model and the stochastic soil water dynamics model and so on. Because meteorology, soil and crops have some random features in time and space, it is difficult to select the modelling parameters to predict [1].
Artificial Neural Network (ANN) is an analysis method dealing with global and nonlinear mapping relationship between inputs and outputs. Because of self-organizing, self-learning and redundant fault-tolerant properties of the input data, ANN has a great advantage in the data fitting and function approximation and have widely been applied [2-4], such as the predication of soil moisture [1,4-6].
As a kind of LAN transformation of time and frequency, Wavelet analysis can extract the information effectively in the signal, and proceeds multi-scale refinement analysis of signal through scaling and translation to realize the high-resolution local positioning of the time domain and frequency domain. Combining with the artificial neural network and wavelet analysis method, wavelet neural network method has two sides of advantages and widely applied in the hydrological forecasting [7], water quality prediction [8] and so on. However, there are a few reports of the application of wavelet neural network method in soil moisture forecast, especially the predict accuracy of soil water content in forest land. In this paper, authors try to use wavelet and neural network model to forecast the soil moisture in caragana shrubland. The results will provide a powerful basis for estimating the soil water resources use limit by plant,soil water carrying capacity for vegetation and the regulation of the relationship between plant growth and soil water and the vegetation restoration in loess hilly region [9].
Site description
This study was carried out at the Shanghuang Eco-experiment Station, located in the semiarid region of the Loess Plateau (35°59′- 36°02′ N, 106°26′- 106°30′E) in Guyuan, Ningxia Hui Autonomous Region. The altitude ranges from 1,534 to 1,824 m above the sea level. Precipitation is scarce in the period from January to March, and the rainfall from June to September accounts for more than 70% of the annual precipitation. Mean rainfall measured between 1983 and 2001 was 415.6 mm with a maximum of 635 mm in 1984 and a minimum of 260 mm in 1991. The frost-free period is 152 days. The soil is mainly loamy loess [10], which is porous and widely distributed in the semiarid region of the Loess Plateau. There is a little change of soil texture with the depth in the soil profile [11]. The experimental field was located in the Caragana bushland in the middle of Heici Mountain with a slope gradient of 3°, facing southeast at the station. The study object is 16-year-old Caragana (Caragana korshinskii) Plantation, under which the main plant species are Stipa bungeana, Heteropappus altaicus, Artemisia giraldii and Thymus mongolicus.
Measurement
The investigation of the existing Caragana shrubs was made at the study site in April of 2002. There are five 100m2 (5×20m) standard runoff plots. The sowing amounts of Caragana were 2.0 kg, 1.5 kg, 1.0 kg, 0.5 kg and 0 kg/100m2 (wasteland, control), respectively. A neutron probe, CNC503A (Beijing Nuclear Instrument Company, Beijing), was used to measure soil moisture in the soil layers from 5 cm to 780 cm and measurement was made at every 20 cm interval. The soil water content obtained for each measuring depth was taken to be representative for the soil layer that included the measuring point ±10 cm depth, apart from that for the 5 cm depth, which was taken to represent the upper 10 cm of soil. Neutron counts were made for 16 seconds. The growing season of Caragana was in the period from April to October every year. Measurement was made at 15 days interval in growing season and one time per month in the period of dormancy. This paper selects the soil water contents measured in the experimental plot with the sowing amount of 1.5 kg /100 as the research object to analysis and predict the dynamics of soil moisture in Caragana brushland.
Data process
The MATLAB software was used to process the data [12]. The data measured in this study basically reflect the soil moisture dynamic change trend, but it is short for neural network training and wavelet analysis, so cubic spline interpolation method was used to enlarge the measure frequency to one time a week and then got 113 sets of data.
Wavelet analysis
Wavelet analysis, a kind of mathematical method based on Fourier analysis, can show the subtle structure and characteristics of measured data using wavelet transform through selecting proper scale and window functions [13]. Wavelet transformation needs to choose suitable wavelet function such as Haar Daubechies Symlets Coiflets and so on. The Daubechies wavelet function can be used to better analyse the problems of time series reported by Zhou & Gui [14].
NARX recursive neural network
Nonlinear Auto-regressive with Exogenous Inputs Model (NARX network) [1] was a kind of recursive neural networks with delay unit and was referred to the nonlinear auto-regressive models with external input. The input layer of the network receives two kinds of signals. The inputs from the outside the network can be expressed as u(k), u(k-1), ..., u(k-p+1), and the outputs of feedback signals from the network can be expressed as y(k), y(k-1),..., y(k-p+1), and the nonlinear system of network dynamic can be expressed as y(k+1) = F(y(k), ..., y(k-p+1), u(k), ..., u(k-p+1)). The NARX network training algorithm adopted LM algorithm of BP network.
Model
Soil water data were divided and reconstruct based on the wavelet analysis method, and then authors got the general picture of the low-frequency components and high -frequency details. In model I, authors selected the low frequency component and the soil water content in a soil layer which is highly correlated with that in the predicted soil layers as input variables to build NARX recursive neural network prediction model I according to wavelet analysis. In Model II: NARX neural network was used to predict the general picture of low-frequency components and high frequency detail respectively, and then we have got the soil moisture forecast results by summing the network outputs.
Selection of target layers
The soil moisture contents in 5 to 300 cm soil layers were selected as the research target. The variation coefficient of soil moisture content in each soil layer were estimated. The variation coefficient of soil moisture content in 5 cm soil layer, CV5 is more than 30%, that is to say, CV5 > 30%, 20% < CV20-80 < 30%, 5% < CV100-180 < 20%, CV200-300 < 5%, respectively, so the 5 to 300 cm soil layers can be classified into four groups, 0 to 5 cm, 20 to 80 cm, 80 to 180 cm and 200 to 300 cm soil layer. Because soil moisture content in the 5 cm soil layer is surface soil and interfered by outside factors and the change trend of soil water in the soil layer was uncertainty in Caragana brushland, it was not be selected as the research target. Finally, the soil water contents in the rest three soil layers such as 40 cm, 100 cm and 200 cm soil layers were chosen respectively as the analysis object.
Wavelet analysis of soil moisture
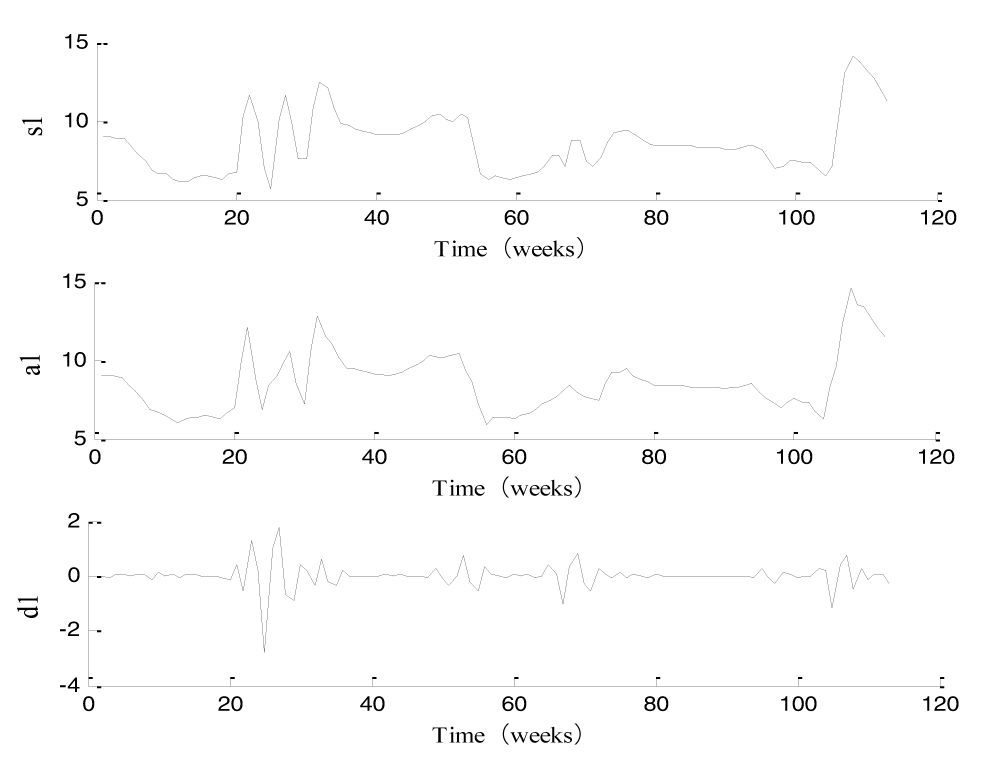
First, the soil water content in the 100 cm layer were selected as the research objects, and the interpolated 113 sets of data in 100 cm layer were selected as the original wavelet sequence s1, then db2 was selected to do single scaling wavelet decomposition and reconstruction [15,16], as shown in Figure 1.
Figure 1: Results of wavelet analysis of soil water content in 100 cm soil layer.
In Figure 1, s1 is time series trend diagram of soil moisture data measured in 100 cm soil layer, a1 is the general picture part of low frequency and its variation trend is consistent with the original signal. The high frequency detail part is d1 after soil water data were decomposed using single scale wavelet, which reflects the change of the original signal frequency. s1, s1= a1+d1, is the synthesized reconstruction signal of decomposed by single scaling wavelet.
The selection of input variable
This article selected the soil moisture content in the soil layers that highly correlated with s1 as the inputs, the correlation results at each soil layer are shown in Table 1. Besides, a1 can be used as an input because it has the similar dynamic change trend with s1, so input variables of model I were as follows: 60 cm, 80 cm, 120 cm, 140 cm, a1 and output variables was s1.
| Table 1: The correlation analysis among soil water contents in 40 cm to 160 cm soil layers. | |||||||
| Soil layer (cm) | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| 40 | 1 | 0.893 | 0.717 | 0.423 | 0.375 | 0.32 | 0.177 |
| 60 | 0.893 | 1 | 0.889 | 0.616 | 0.525 | 0.416 | 0.228 |
| 80 | 0.717 | 0.889 | 1 | 0.683 | 0.62 | 0.51 | 0.323 |
| 100 | 0.423 | 0.616 | 0.683 | 1 | 0.892 | 0.711 | 0.229 |
| 120 | 0.375 | 0.525 | 0.62 | 0.892 | 1 | 0.923 | 0.431 |
| 140 | 0.32 | 0.416 | 0.51 | 0.711 | 0.923 | 1 | 0.598 |
| 160 | 0.177 | 0.228 | 0.323 | 0.229 | 0.431 | 0.598 | 1 |
The selection of input variables in model II: (1) when predicting a1, the soil water contents in 60 cm, 80 cm, 100 cm, 120 cm and 140 cm soil layers were inputs, a1 was outputs; (2) when when predicting d1, s1 is only related to s1, d1 was output variable.
Comparison between model I and model II
The range of soil moisture content was volatile due to much affecting factors, so this article was only used for short-term prediction. The input variables of week N and output variables of week N + 1 form a sample set, and there was a total of 112 samples sets. Data sets was divided as follows: the data from 1 to 90 groups was taken as the training set, which used for fitting model; the data from 91 to 101 sets was taken as the validation set , which used for the prediction of error estimation in the selected model; the remaining data in II sets be used as a test set to ultimately evaluate the generalization error of selected model.
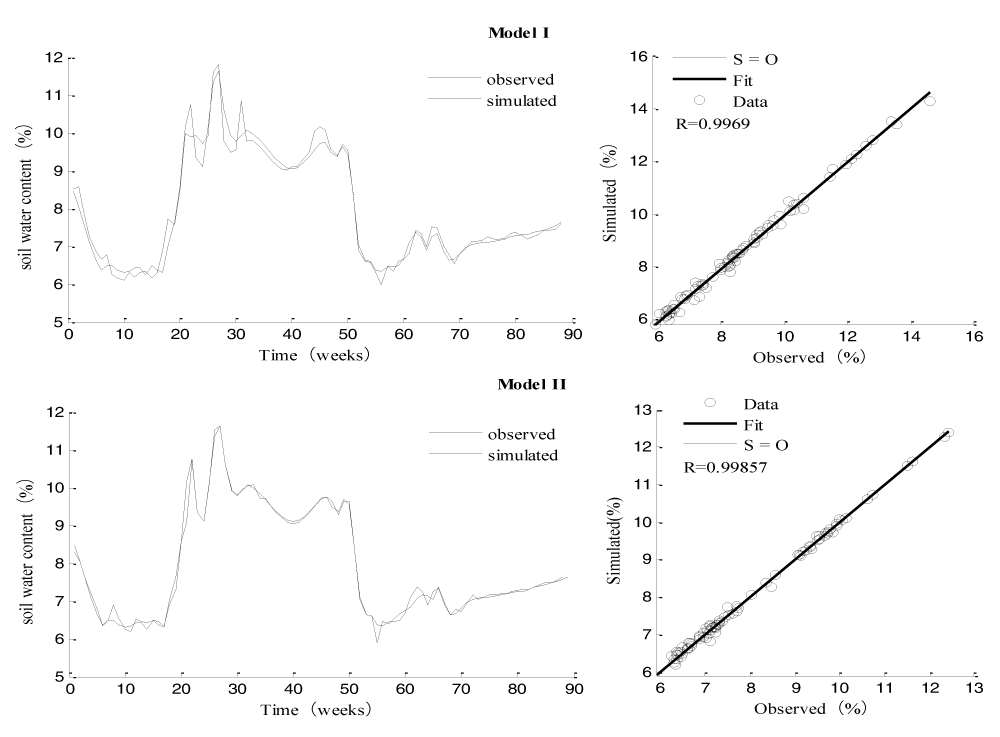
Figure 2 showed the simulation correlation analysis in training set s1 for model I and model II. Of d1 is only related to s1, d1 was output variable. It can be seen from Figure 2 that model II was better than model I in the overlap of the simulated values predicting d1, s1 was input variable for the change and the measured values and in the correlation analysis, showing that the NARX recursive neural network has better learning. Ability than BP neural network.
Figure 2: Correlation analysis of simulated values in 100 cm soil layer.
Table 2 is the validation set of forecast error analysis for the model I and model II. It can be seen from the Table 2 that average relative error of model I was 3.5% and that of model II was 0.3%, showing that the prediction accuracy using the model II was higher than that using model I.
| Table 2: Comparison of predicted error of validation set. | |||
| Items | Relative error (%) | Items | Relative error % |
| 92 | 6.99 | 99 | -3.27 |
| 93 | 5.98 | 100 | -4.75 |
| 94 | 6.27 | 101 | 2.68 |
| 95 | 10.90 | 102 | 4.77 |
| 96 | 5.56 | Average relative error (%) | 3.52 |
| 97 | -0.08 | ||
| 98 | 3.66 | ||
The applicant of model II
In order to study the feasibility of actual operation of model II, in the paper soil water content from 103 to 113 weeks in the 100 cm soil layer were forecasted, as shown in Table 3.
| Table 3: Comparison of predicted error and observed values from 103 to113 week in 100 cm soil layer. | |||
| Week | Observed | Week | Observed |
| 103 | 6.8622 | 6.8836 | 0.31 |
| 104 | 6.8289 | 6.8951 | 0.97 |
| 105 | 6.6937 | 6.7091 | 0.23 |
| 106 | 6.4809 | 6.4841 | 0.05 |
| 107 | 7.1149 | 7.1138 | -0.02 |
| 108 | 9.2415 | 9.2373 | -0.05 |
| 109 | 11.4952 | 11.5012 | 0.05 |
| 110 | 12.4359 | 12.4043 | -0.25 |
| 111 | 12.3375 | 12.2879 | -0.40 |
| 112 | 11.9021 | 11.3647 | -4.52 |
| 113 | 11.8320 | 12.0770 | 2.07 |
| Average relative error (%) | 0.81 | ||
Based on wavelet analysis, the model II was more suitable than model I for forecasting soil water content in the Caragana shrubland by comparing the results of correlation analysis of simulated and measured values and the prediction error analysis of validation set.
The average relative error of predicted soil water from 103 to 113 weeks is 0.8%, and absolute values of relative error of soil water in the 11 weeks’soil water were lower than 10%, showing that model is feasible in prediction of soil water content in the woodland.
The model after training (learning) right reflects the samples that did not occurred in training set. Learning is not simply to memorize the studied inputs, but to learn the inner regularity of environment itself embedded in the sample through the study of a finite number of being trained samples16. To further test the model generalization ability, moisture contents from 103 to 113 weeks in 40 cm and 200 cm soil layer were predicted. The error analysis of prediction values was shown in Table 4.
| Table 4: Error analysis of the predicted values from 103 to 113 week at 40 cm and 200 cm soil layers. | ||||||
| Items | 40 cm | 200 cm | ||||
| Week | Actual data | Week | Actual data | Week | Actual data | Week |
| 103 | 6.862 | 6.4253 | -6.37 | 6.314 | 6.2957 | -0.30 |
| 104 | 6.123 | 5.9140 | -3.41 | 6.327 | 6.2908 | -0.57 |
| 105 | 6.704 | 6.2114 | -7.35 | 6.357 | 6.3538 | -0.05 |
| 106 | 13.05 | 12.66 | -3.02 | 6.358 | 6.3704 | 0.20 |
| 107 | 16.73 | 16.518 | -1.26 | 6.399 | 6.3696 | -0.46 |
| 108 | 17.48 | 17.353 | -0.74 | 6.537 | 6.5047 | -0.49 |
| 109 | 13.78 | 12.784 | -7.23 | 6.652 | 6.6998 | 0.72 |
| 110 | 13.43 | 15.053 | 12.06 | 6.627 | 6.6682 | 0.63 |
| 111 | 11.96 | 12.717 | 6.35 | 6.525 | 6.5400 | 0.23 |
| 112 | 11.05 | 10.554 | -4.45 | 6.455 | 6.4755 | 0.31 |
| 113 | 9.389 | 9.7211 | 3.53 | 6.525 | 6.4913 | -0.52 |
| Average error (%) 4.94 | Average error (%) 0.41 | |||||
It is showed from Table 4 that the curves of predicted values were consistent with the measured values in 40 cm and 200 cm soil layer. The correlation coefficient of the linear regression equation was 0.981, 0.984 respectively, and p < 0.05. The average relative errors were less than 5%, suggesting that the wavelet neural network model II has good generalization performance.
After the original signal were divided into low-frequency components and high-frequency components, wavelet analysis was used to analyse the data, and fully highlighted the trend and frequency fluctuations of signals changing with time, and avoided bad learning problems of some high-frequency mutation data when directly using neural network to predict the original data.
The low-frequency component of the soil water content after wavelet analysis in the soil layers largely correlated with that were selected as the input variables in Model I to predict soil general picture of the low-frequency water content in target soil layer. Model II used NARX recursive neural network to predict the component and high frequency detail component, then combined the outputs. Because of higher fitting precision and smaller error compared with the model I after training analysis and error analysis of verification set, model II can better predict soil moisture content in the Caragana brushland of loess hilly-gully region.
There were different change degrees of soil moisture in each soil layer. The changes of soil moisture content with soil depth gradually tend to be steady. The soil moisture in 100 cm soil layer was selected to forecast soil water content in other soil layers, and the soil moisture in 40 cm and 200 cm soil layer were chose to generalize the model. All of obtained results were ideal.
If we obtain the maximum infiltration depth and the change of withering coefficient with soil depth and soil water resources use limit by plant, the amount of water stored within the maximum infiltration depth, in which the soil moisture content in each layer is equal to the withering coefficient before forecasting soil water content in the the maximum infiltration depth in advance, we can estimate soil water resources within the maximum infiltration depth and then compare the soil water resources and soil water resources use limit by plant. If the soil water resources equal to soil water resources use limit by plant, soil drought is serious. At this stage of plant growth, the soil water seriously influences plant growth. The serious soil drought will cause soil degradation, plant death, crop failure, or waste land resource. In order to control the serious soil drought and obtain high production, we have to predict soil moisture content in the maximum infiltration depth and estimate soil water resources and soil water carrying capacity for vegetation, and then regulate the plant water relationship and improv the soil water condition by reducing plant density to increase the soil water supply from rainfall and reduce the soil water consumption if the soil water resources and soil water resources use limit by plant because soil water resources are renewable resources and only come from rainfall, there is not enough water resource to irrigation, and ground water is deep and cannot be used by plant.When regulate the relationship between soil water and plant growth, the amount of regulation equal the difference between present density minus soil water carrying capacity for vegetation to realize sustainable use of soil water resources [10].
According to the wavelet analysis, NARX recursive neural network model established in this paper has higher prediction accuracy of soil water content, and can well predict soil moisture content at a given soil layers with various fluctuating frequency, and has better generalization performance. This is a good model to predict soil moisture in the brushland. The results provide powerful basis for soil drying control, regulation of the relationship between soil moisture and plant growth and sustainable use of soil water in the water-limited regions.
If we measured the soil water content in the maximum infiltration depth and the change of wilting coefficient with soil depth, and estimated soil water resources, soil water resources use limit by plants in advance before predict soil water at a given soil layers, then we can take effective measure to control the soil degradation and vegetation decline by regulating the relationship between soil moisture and plant growth and realize the sustainable use of soil water and high quality development in the water-limited regions. This research needs to continue.
This study was supported by the National Science Fund of China (Project No. 41271539, 41071193) and National key R & D plan (Project No. 2016YFC0501702).
- Liu HB, Wu W, Wei CF. Study of soil water forecast with neural network. J Soil Water Conserv. 2003;17:59-62. Available from: http://stbcxb.cnjournals.com/stbcxben/article/abstract/200305221
- Zhao L, Shui P, Jiang F, Qiu H, Ren S, Li Y, et al. Using monitor data of surface soil to predict whole crop-root zone soil water content with PSO-LSSVM, GRNN, and WNN. Earth Sci Inform. 2014;7:59–68. Available from: https://link.springer.com/article/10.1007/s12145-013-0130-6
- Pisoni E, Farina M, Carnevale C, Piroddi L. Forecasting peak air pollution levels using NARX models. Eng Appl Artif Intell. 2009;22:593-602. Available from: https://doi.org/10.1016/j.engappai.2009.04.002
- Cai L, Ma SY, Cai HT, Zhou YL, Liu R. Prediction of SYM-H index by NARX neural network from IMF and solar wind data. Sci China Ser E Technol Sci. 2009;52:2877-2885. Available from: https://link.springer.com/article/10.1007/s11431-009-0296-9
- Liu HB, Xie DT, Wu W. Soil water content forecasting by ANN and SVM hybrid architecture. Environ Monit Assess. 2008;143:187-193. Available from: https://link.springer.com/article/10.1007/s10661-007-9967-9
- Guo QC, He ZF. Forecast model of soil water content based on artificial neural network. J Shanxi Agric Sci. 2012;40:892-895.
- Kseneman M, Gleich D, Božidar P. Soil-moisture estimation from TerraSAR-X data using neural networks. Mach Vis Appl. 2012;23:937-952. Available from: https://link.springer.com/article/10.1007/s00138-011-0375-3
- Xu TB, Ma GW, Huang WB, et al. BP network prediction model and its application in annual runoff forecasting based on wavelet analysis. Water Resour Power. 2012;30:17-19.
- Guo Z. Soil hydrology process and sustainable use of soil water resources in desert regions. Water. 2021;13(17):2377. Available from: https://doi.org/10.3390/w13172377
- Lu ZJ, Zhu L, Pei HP. The model of chlorophy II-a concentration forecast in the West Lake based on wavelet analysis and BP neural networks. Chinese J Ecol. 2008;28:4965-4973.
- FAO/UNESCO. Soil map of the world, revised legend. Rome: FAO/UNESCO; 1988.
- Jiang X, Liu H. Radial basis function networks based on wavelet analysis for the annual flow forecast. J Appl Sci. 2004;22:411-414.
- Zhang DF. MATLAB wavelet analysis. 2nd ed. Beijing: Mechanical Industry Press; 2012.
- Yang WZ, Shao MA. Study on soil moisture in the Loess Plateau. Beijing: Science Press; 2000.
- Zhou W, Gui L, Zhou L. High-level technology of MATLAB wavelet analysis. Xi’an: Xidian University Press; 2006. p. 51-63.
- Shi Y, Han LQ, Lian XQ. Neural network design and instance analysis. Beijing: Beijing University of Posts and Telecommunications Press; 2009.